2021年电气工程师《(供配电)公共基础+专业基础》考试题库-(供配电)公共基础-第七节 概率与数理统计-
建筑工程-电气工程师
单选题-已知A为奇数阶实矩阵,设阶数为n,且对于任一n维列向量X,均有XTAX=0,则有( )。
单选题
A.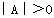
B.
C.
D.以上三种都有可能
我个人认为这个应该是:B
解析:由于对任一n维列向量均有XTAX=0,两边转置,有XTATX=0,从而XT(A+AT)X=0。显然有(A+AT)T=A+AT,即A+AT为对称矩阵。从而对任一n维列向量均有:XT(A+AT)X=0,A+AT为实对称矩阵,从而有A+AT=0。即AT=-A,从而A为实反对称矩阵,且A为奇数阶,故|A|=0。
本文来自zhongtiku投稿,不代表升华网立场,如若转载,请注明出处:http://54sh.com/zhiyetiku/491660.html

